
где f(mT) – решетчатая функция оригинал, F*(p) –дискретное изображение Лапласа, m = 0,1,2,3,… - целочисленный параметр, D – символическое обозначение дискретного преобразования Лапласа.
Обратное дискретное преобразование Лапласа
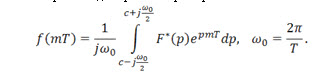
Символика обратного дискретного преобразования Лапласа
![]()
Для идентификации дискретного изображения Лапласа функции изображения помечаются «звездочкой».
Связь между изображениями дискретного и непрерывного преобразования
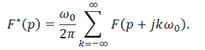
Последнее выражение связывает изображения непрерывной F(р) и решетчатой функций F*(р). Операция нахождения дискретного изображения F*(р) по не-прерывному изображению F(р) называется D – преобразованием (D - готическое).
Пример. Найдем дискретное изображение Лапласа для константы f(mT)=A
![]()
![]() –геометрическая прогрессия со знаменателем . Сумма членов этой геометрической прогрессии
–геометрическая прогрессия со знаменателем . Сумма членов этой геометрической прогрессии
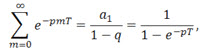
где a1 – первый член прогрессии (m=0).
Следовательно
![]()
Дискретные изображения Лапласа являются функциями epTи вид их сложнее по сравнению с непрерывными изображениями.
Я последнее время плохо спала, потому что мучали боли в шейном отделе и все-таки нашла этому решение - ортопедическая подушка для сна. Мне ее купить посоветовала мама. И теперь нет никаких проблем.
