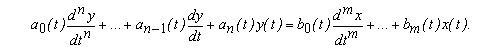Описать свойства системы в этом случае можно через функцию веса, которая получается путем решения дифференциального уравнения системы при входном воздействии, описываемом единичной импульсной функцией (дельта-функцией)
![]()
Решая дифференциальное уравнение системы с переменными коэффициентами при x(t)=σ(t),получим функцию веса системы с переменными параметрами
![]()
В выражение для функции веса входит параметр времени
Если известна функция веса системы с переменными параметрами, то можно определить процесс в системе при любом входном воздействии x(t).
![]()
Из последнего выражения видно, что для нахождения переходного процесса необходимо знать функцию веса системы. Функция веса системы с переменными параметрами является исчерпывающей ее характеристикой.
Функция веса находится путем решения дифференциального уравнения. В общем виде решение дифференциального уравнения с переменными коэффициентами возможно для уравнений первого и второго порядка.
В соответствие с теорией обыкновенных линейных систем функция веса является функцией–оригиналом для передаточной функции системы. Если распространить это положение на системы с переменными параметрами, то можно формально определить передаточную функцию системы подвергнув преобразованию Лапласа функцию веса системы.
![]()
В полученное выражение для передаточной функции входит временной параметр и поэтому она называется параметрической.
При известной параметрической передаточной функции системы можно описать переходный процесс в системе с переменными параметрами, который будет зависеть не только от возмущения, но и от момента его приложения.
![]()
Применяя параметрическую передаточную функцию системы с переменными параметрами или ее функцию веса, можно произвести исследование устойчивости и качества переходного процесса системы теми же методами, которые используются для линейных обыкновенных систем автоматического управления.