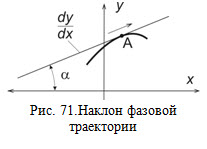
 Для исключения необходимости решения дифференциального уравнения при построении фазовых траекторий используется метод изоклин. На рис. 71 показан фрагмент фазовой траектории. Если рассматривать произвольную точку A фазовой траектории, то направление траектории в этой точке можно определить, проведя касательную к фазовой траектории в рассматриваемой точке. Для этой касательной
Для исключения необходимости решения дифференциального уравнения при построении фазовых траекторий используется метод изоклин. На рис. 71 показан фрагмент фазовой траектории. Если рассматривать произвольную точку A фазовой траектории, то направление траектории в этой точке можно определить, проведя касательную к фазовой траектории в рассматриваемой точке. Для этой касательной
![]()
Таким образом, направление фазовой траектории в произвольной ее точке можно задать углом наклона α касательной, проведенной к фазовой траектории в этой точке. Вместо угла наклона удобнее использовать константу c. Если на фазовой плоскости соединить линией все точки, в которых фазовая траектория имеет одинаковое направление (одно и то же значение константы c), то мы получим изоклину – линию равных углов наклона касательной к фазовой траектории.
Уравнение изоклины
c=f(x,y),
где f(x,y) – правая часть дифференциального уравнения фазовой траектории.
Например, если дифференциальное уравнение фазовой траектории
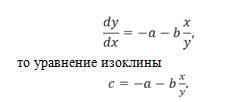
Уравнение изоклины алгебраическое. Задавая разные значения константы можно построить семейство изоклин на фазовой плоскости, каждая из которых характеризует определенное направления фазовой траектории. Пример построения семейства изоклин приведен на рис. 72. Стрелками указано направление фазовой траектории в точках изоклины.
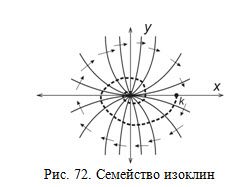 Для построения фазовой траектории задают ее начальную точку, соответствующую начальным условиям для исследуемой системы (точка k на рис. 72). Затем из этой точки проводят отрезок прямой в сторону ближайшей изоклины параллельно стрелке, определяющей направление фазовой траектории в точках этой изоклины. Линия проводится примерно до середины промежутка между изоклинами.
Для построения фазовой траектории задают ее начальную точку, соответствующую начальным условиям для исследуемой системы (точка k на рис. 72). Затем из этой точки проводят отрезок прямой в сторону ближайшей изоклины параллельно стрелке, определяющей направление фазовой траектории в точках этой изоклины. Линия проводится примерно до середины промежутка между изоклинами.
Конец отрезка принимают за начальную точку следующего отрезка, который строят по описанному алгоритму. Полученная ломаная линия сглаживается до получения линии фазовой траектории.
Метод изоклин прост, т.к. не требует решения дифференциального уравнения. Однако, он требует значительного объема графических построений. Одновременно метод изоклин является методом приближенного построения фазовых траекторий, что следует учитывать при его использовании.
Если вы задумали построить дом из бруса, но у вас нет информации достаточной об этом, то перейдите по этой ссылке http://www.baniizpestovo.ru/ - это отличный сайт, где вы найдете для себя много полезной информации.






